Calculating Geodesic distance – solutions to an Earthly problem

11/18/2021

Recently I had a requirement to get the great circle distance (GCD) between two points on earth. I needed to calculate ‘as the crow flies’ distance between a pair of latitude/ longitude provided. Since this was new to me, I did some research to figure out what my options are. It seems there has been a lot of research that went into this and there are quite a number formulas that can be used.

Calculating geodesic distance, as it is called, is required for navigation applications. We use GCD (great circle distance) to estimate flight time between two locations. It is also used for celestial distance measurement. We can use various available mathematical formulas to calculate this distance. For this blog, I decided to provide the python implementation for three such formulas. One thing to remember is that this assumes a flat earth surface. So you have to float over oceans and dig through mountains to match this distance.

Law of Cosines

I will start with the easiest formula for this problem known as ‘law of cosines’. This is a mathematical formula that accurately provides the length of the chord that joins the two points. This formula converts over to Pythagorean formula when angle if 90 degrees.Given that we want to travel between two points,

\angle A = sin(\psi_1) * sin(\psi_2)
\angle B = cos(\psi_1) * cos(\psi_2) * cos(\lambda_2 - \lambda_1)
\angle \theta = arccos(\angle A + \angle B)
d = R * \angle \theta

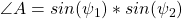
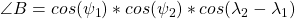
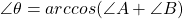
* All angles are in radians
\psi: Latitudes (1 and 2)
\lambda: Longitudes
\theta: Angle formed at center by these points
d: Distance between the points
R: Mean radius of Earth

The primary issue with this approach is that it assumes that earth is spherical. Also, based on what I have read online, for short distances it is not as accurate either.

Since we will use all angles as Radians, we will convert them to radians as soon as class initializes.

def __init__(self, point_a: tuple, point_b: tuple):
  self.point_A_lat = radians(point_a[0])
  self.point_A_lon = radians(point_a[1])
  self.point_B_lat = radians(point_b[0])
  self.point_B_lon = radians(point_b[1])
def calc_distance(self):
  ang_A = sin(self.point_A_lat) * sin(self.point_B_lat)
  ang_B = cos(self.point_A_lat) * cos(self.point_B_lat) * cos(self.point_B_lon - self.point_A_lon)
  ang_C = acos(ang_A + ang_B)
  dist = MEAN_RADIUS * ang_C
  print('Distance by Law of Cosines: %.2f m or %.2f miles' % (dist, dist * 0.0006213712))
  return dist

Above code is self explanatory. We are following the exact steps that I have provided above.

Haversine

Haversine, or half versed sine, is one more formula that is used to calculate the straight line distance between two coordinates on earth. This also assumes that earth surface is a round as the basketball.

sin^2(\frac d {2R}) = sin^2(\frac {\psi_2 - \psi_1} 2) + cos(\psi_1) * cos(\psi_2)*sin^2(\frac{\lambda_2-\lambda_1} 2)

which gives us:

d = 2R sin^{-1}(\sqrt{sin^2(\frac {\psi_2 - \psi_1} 2) + cos(\psi_1) * cos(\psi_2)*sin^2(\frac{\lambda_2-\lambda_1} 2)})

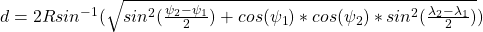
That is not the easiest formula, but it does give better results apparently than law of cosines. We provide below the implementation in Python.

def calc_distance(self):
  delta_lat = self.point_B_lat - self.point_A_lat
  delta_lon = self.point_B_lon - self.point_A_lon
  haversine_val = (sin(delta_lat * 0.5) ** 2) + (sin(delta_lon * 0.5) ** 2) * \
  cos(self.point_A_lat) * cos(self.point_B_lat)
  dist = 2 * MEAN_RADIUS * asin(sqrt(haversine_val))
  print('Distance by Haversine: %.2f m or %.2f miles' % (dist, dist * 0.0006213712))
  return dist

Here we calculate the delta for latitude and longitude first. Next we calculate the value for d/2R sine squared. Finally, we calculate the distance. In this case we also take mean earth radius for calculation.

Vincenty’s formula

Vincenty’s formula was first derived by Thaddeus Vincenty. This formula will give the most accurate results of all as it considers the flatness of the earth. We calculate the polar radius of the earth assuming a flatness correction factor of 1/298.25722. This means that earth is flatter towards the pole and bulges towards the equator.

There are two different formulae provided by Vincenty, Direct and Inverse. We need direct when we know one point and the distance. In this case we will find out the second point on earth. However, for our problem, we are interested in Inverse formula. We use the inverse formula when we need to calculate the distance between two given points.

Please refer to Wikipedia for Vincenty’s formula here. I am using a screenshot from Wikipedia here for reference. I have no intent to write all these equations in tex :).

© Wikipedia.com, used for reference only

This is the longest code that we need to calculate geodesic distance.

def calc_distance(self):
  val_l = self.point_B_lon - self.point_A_lon
  val_u1 = atan((1 - FLAT_CORRECT) * tan(self.point_A_lat))
  val_u2 = atan((1 - FLAT_CORRECT) * tan(self.point_B_lat))

  val_sin_u1 = sin(val_u1)
  val_cos_u1 = cos(val_u1)
  val_sin_u2 = sin(val_u2)
  val_cos_u2 = cos(val_u2)

  val_lambda = val_l

  cos_sq_alpha = None
  val_sigma = None
  sin_sigma = None
  cos_sigma = None
  cos2_sigma_m = None
  for i in range(0, Vincenty.max_iters):
    i += 1

    sin_lambda = sin(val_lambda)
    cos_lambda = cos(val_lambda)
    sin_sigma = sqrt((val_cos_u2 * sin(val_lambda)) ** 2 +
                     (val_cos_u1 * val_sin_u2 - val_sin_u1 * val_cos_u2 * cos_lambda) ** 2)
    cos_sigma = val_sin_u1 * val_sin_u2 + val_cos_u1 * val_cos_u2 * cos_lambda
    val_sigma = atan2(sin_sigma, cos_sigma)
    sin_alpha = (val_cos_u1 * val_cos_u2 * sin_lambda) / sin_sigma
    cos_sq_alpha = 1 - sin_alpha ** 2
    cos2_sigma_m = cos_sigma - ((2 * val_sin_u1 * val_sin_u2) / cos_sq_alpha)
    val_c = (FLAT_CORRECT / 16) * cos_sq_alpha * (4 + FLAT_CORRECT * (4 - 3 * cos_sq_alpha))
    val_lambda_prv = val_lambda
    val_lambda = val_l + (1 - val_c) * FLAT_CORRECT * sin_alpha * \
    (val_sigma + val_c * sin_sigma * (cos2_sigma_m + val_c * cos_sigma * (-1 + 2 * cos2_sigma_m ** 2)))

    val_diff = abs(val_lambda_prv - val_lambda)
    if val_diff <= Vincenty.tolerance:
      break

      val_u_sq = cos_sq_alpha * ((EQTR_RADIUS ** 2 - POLR_RADIUS ** 2) / POLR_RADIUS ** 2)
      val_a = 1 + (val_u_sq / 16384) * (4096 + val_u_sq * (-768 + val_u_sq * (320 - 175 * val_u_sq)))
      val_b = (val_u_sq / 1024) * (256 + val_u_sq * (-128 + val_u_sq * (74 - 47 * val_u_sq)))
      delta_sig = val_b * sin_sigma * (cos2_sigma_m + 0.25 * val_b * (
        cos_sigma * (-1 + 2 * cos2_sigma_m ** 2) - (1 / 6) * val_b * cos2_sigma_m * (
          -3 + 4 * sin_sigma ** 2) * (-3 + 4 * cos2_sigma_m ** 2)))
      dist = POLR_RADIUS * val_a * (val_sigma - delta_sig)
      print('Distance by Vincenty: %.2f m or %.2f miles' % (dist, dist * 0.0006213712))
      return dist

As I said before, this will provide the most accurate result. However, we have to perform a lot more calculation here. So, if you do not need very accurate results and lean towards performance, you can use the other equations.

Comparison

We will run a few comparison and see what value we get between each of them (in miles).

DestinationLaw of CosinesHaversineVincenty
Milan to Paris397.3939397.3939398.1266
New York to new Delhi7304.05847304.05847317.9312
BC to Abu Dhabi7033.69367033.69367046.7748
Kolkata to Berlin2478.07662478.07662485.7594
Kenya to Auckland8633.29398633.29393795.4240

Everything seems to be aligning nicely. However, we see a drastic difference in the calculation between Kenya and Auckland. On investigation, it looks like the numbers returned by Haversine/ Law of Cosines is much closer to the actual. If I calculate it on distance calculator website,

However, the Vincenty’s answer also matches when I test it on WGS-84 website.

I do not know why there is a mismatch. I will try to find out and if I can, I will update the blog.

For completeness, here is the output from code.

Calculating distance between Milan & Paris [(48.85341, 2.3488) -> (45.46427, 9.18951)]:
Distance by Law of Cosines: 639543.4029 m or 397.3939 miles
Distance by Haversine: 639543.4029 m or 397.3939 miles
Distance by Vincenty: 640722.6394 m or 398.1266 miles

Calculating distance between NY & New Delhi [(40.712776, -74.005974) -> (28.613939, 77.209023)]:
Distance by Law of Cosines: 11754742.3641 m or 7304.0584 miles
Distance by Haversine: 11754742.3641 m or 7304.0584 miles
Distance by Vincenty: 11777068.5849 m or 7317.9312 miles

Calculating distance between BC & Abu Dhabi [(53.726669, -127.647621) -> (24.453884, 54.377342)]:
Distance by Law of Cosines: 11319632.4995 m or 7033.6936 miles
Distance by Haversine: 11319632.4995 m or 7033.6936 miles
Distance by Vincenty: 11340684.6690 m or 7046.7748 miles

Calculating distance between Kolkata & Berlin [(88.363895, 22.572646) -> (52.520008, 13.404954)]:
Distance by Law of Cosines: 3988077.6989 m or 2478.0766 miles
Distance by Haversine: 3988077.6989 m or 2478.0766 miles
Distance by Vincenty: 4000441.9305 m or 2485.7594 miles

Calculating distance between Kenya & Auckland [(37.906193, -0.023559) -> (174.763331, -36.84846)]:
Distance by Law of Cosines: 13893939.4862 m or 8633.2939 miles
Distance by Haversine: 13893939.4862 m or 8633.2939 miles
Distance by Vincenty: 6108142.8142 m or 3795.4240 miles

Process finished with exit code 0

As always you can find the source codes at github/chakrab. Ciao for now!